あめ

ブログです．

面積を求める

数学

関数が囲む面積{S}を求めてみましょう。


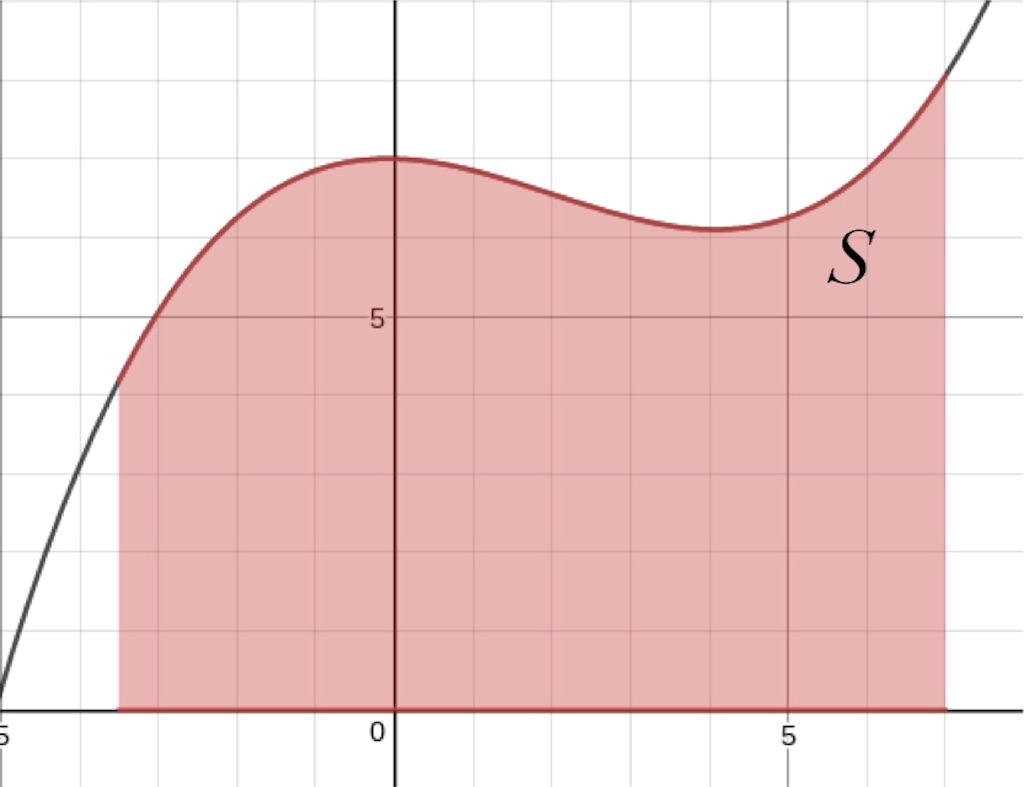
面積を求めるといえば、

{ \displaystyle S=\int_a^bf(x)dx }

やっぱり積分を思い浮かべます。後で説明するので、今は「{\int}って招き猫の手みたいだな」くらいに思っておけば大丈夫です。

{f(x)}は関数の名前です。関数{f}は{x}で決まる、という意味。{f}は{function}の頭文字です。

高校では微分の逆演算として習う積分ですが、微分が変化を求めるのに対し、積分は細く足すという意味です。あまり逆って感じはしませんね。

それもそのはずで、積分は本来、区分求積によって定義されます。詳しく見ていきましょう


区分求積


「じゃあ区分求積って何さ」ってなります。

区分求積とは、区分けして面積を求めるという意味です。
文字通りの意味でわかりやすいです。

こんなイメージ


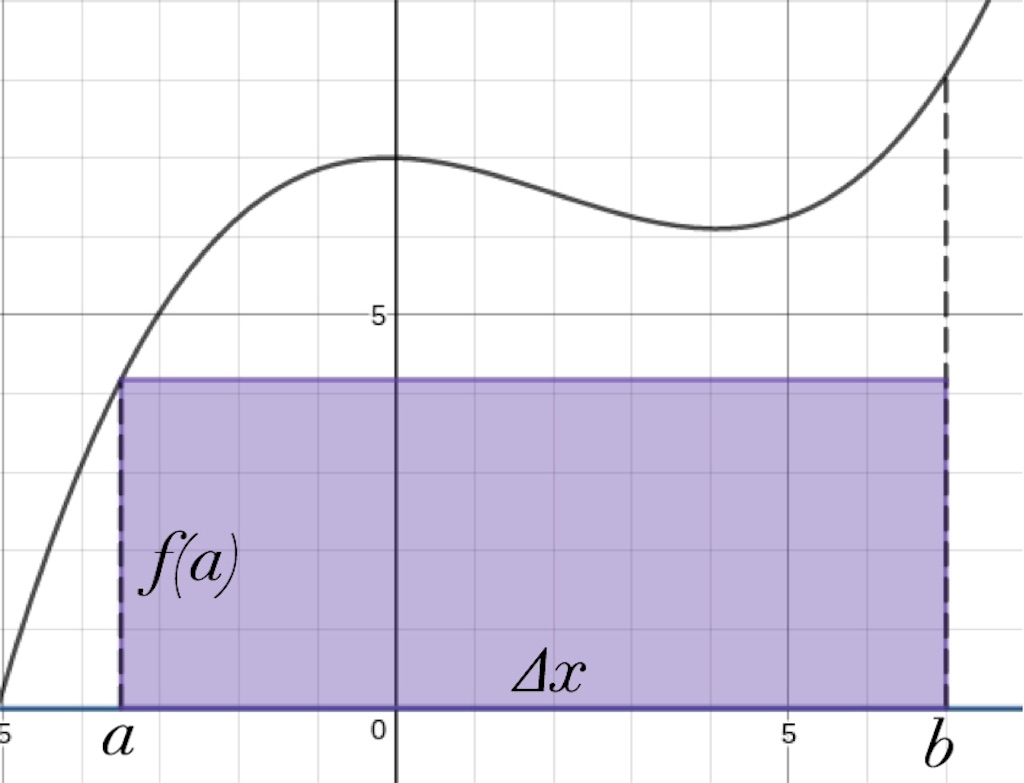
「いや、面積全然違うやん」って思いましたか？

ひとまず、この面積を式で書いてみましょう。左右の端の{x}座標をそれぞれ{a,b}、長方形の面積を{S_1}、長方形の底辺の長さを{\Delta x_1=\frac{b-a}1}として、

{ \displaystyle S_1=f(a)\Delta x_1 }

となります。{f(a)}は{x=a}のときの関数{f}の値。

長方形の面積{=}底辺{×}高さ

ですね。

では、もう少し細く分けてみましょう。


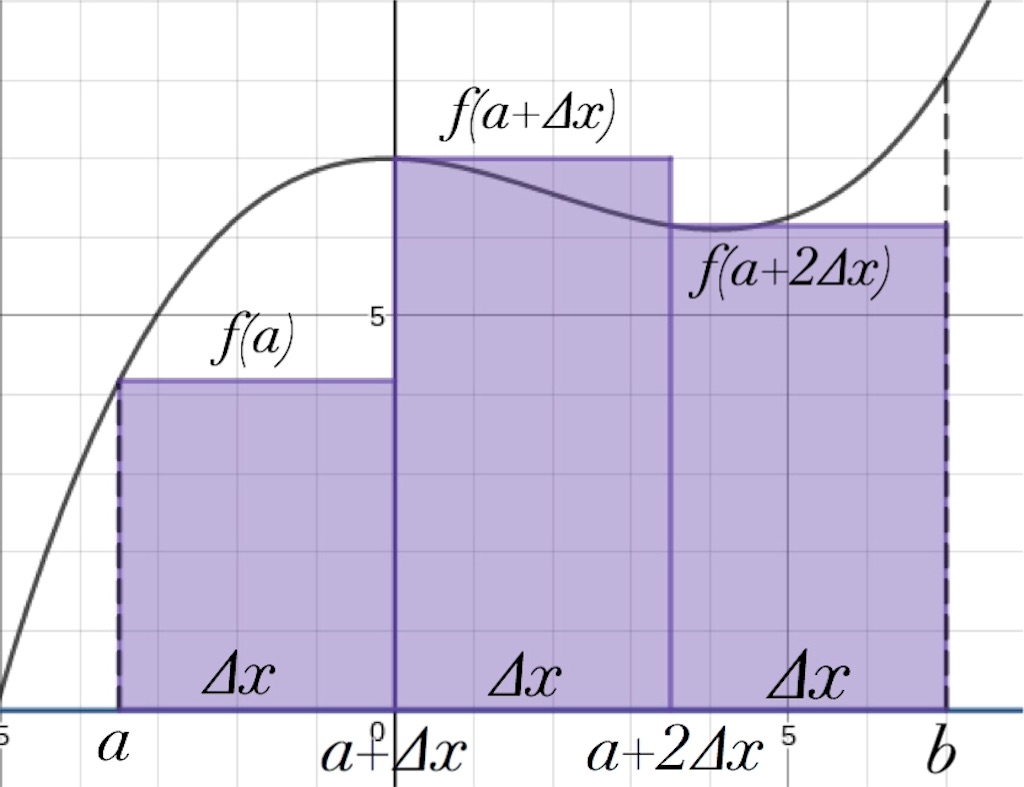
さっきよりも良い感じ。

先ほどと同様に考えてみましょう。

三つの長方形の面積の合計を{S_3}、一つの長方形の底辺の長さを{\Delta x_3=\frac{b-a}3}として、

{ \displaystyle S_3=\Delta x_3 \left\{f(a)+f(a+\Delta x_3)+f(a+2\Delta x_3)\right\} }

煩雑で見にくいので、足し算の省略記号{\Sigma}(シグマ)を使って書いてみましょう。

{ \displaystyle S_3=\sum_{k=0}^2 f(a+k\Delta x_3 )\Delta x_3 }

{k=0,k=1,k=2}をそれぞれ代入した時の和を意味しています。

もう気づいたかもしれませんが、区分けをもっと細くすると求める面積に近づきそうです。


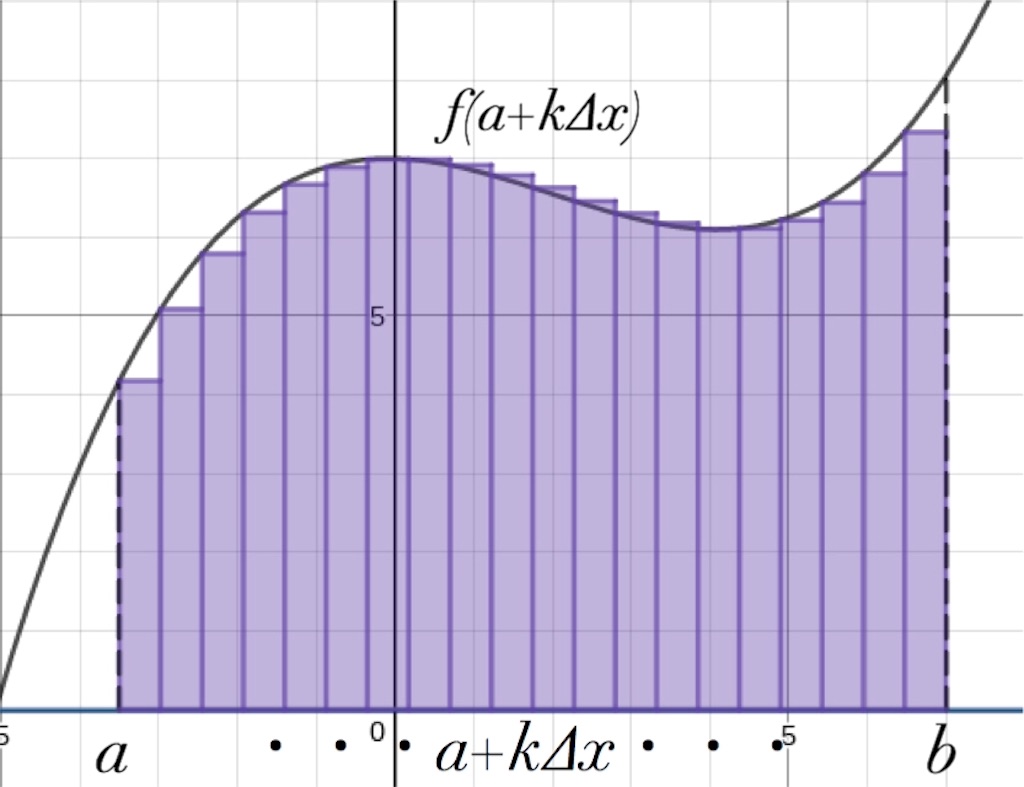
それでは、一般化して書いてみましょう。{n}個の長方形の面積の合計を{S_n}、一つの長方形の底辺の長さを{\Delta x_n=\frac{b-a}n}、として、

{ \displaystyle S_n=\sum_{k=0}^{n-1} f(a+k\Delta x_n )\Delta x_n }

と書けますね。足し算は{\Sigma}で省略しています。

結論として、{n \rightarrow \infty}として限りなく細くすれば、{S_n \rightarrow S}となり関数の囲む面積に収束します。

遊べます


好きな関数で区分求積できるグラフを作りました。下記URL

区分求積法-Desmos

から実際に動かせます。{f(x)=}以降の部分を消して、好きな関数を入力してみてください。パラメータ{n}の値を大きくすれば、長方形が細くなっていきます。グラフ内の点をドラッグして操作することもできます。

積分


先ほど、区分求積による面積を

{ \displaystyle S_n=\sum_{k=0}^{n-1} f(a+k\Delta x_n )\Delta x_n }

と書きましたね。{n \rightarrow \infty}と書いて{n}を限りなく大きくすると、

{ \displaystyle S=\sum_{k=0}^\infty f(a+k\Delta x_\infty )\Delta x_\infty }

と表せそうです。{\Delta x_n =\frac{b-a}n}だったので、{\Delta x_\infty}は限りなく{0}に近くなります。このとき、{\Delta x_\infty =dx}と書き換えてみましょう。

また、{\Delta x_\infty}が限りなく小さいのでこの面積Sは{f(x)}\Delta x_\inftyを{x=a}から{x=b}まで細く足しあわせた値になりそうです。

これで、始めに言った積分の定義とつながりました。

{ \displaystyle \lim_{n \rightarrow \infty} \sum_{k=0}^{n-1} f(a+k\Delta x_n )\Delta x_n =\int_a^bf(x)dx }

どうでしょうか？